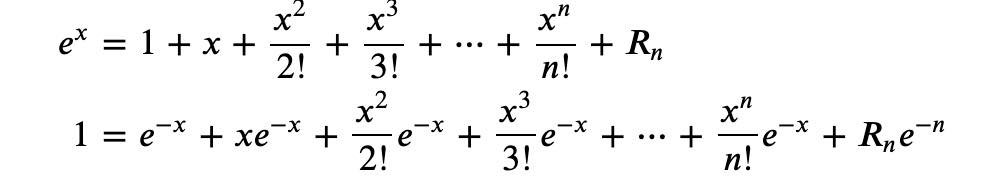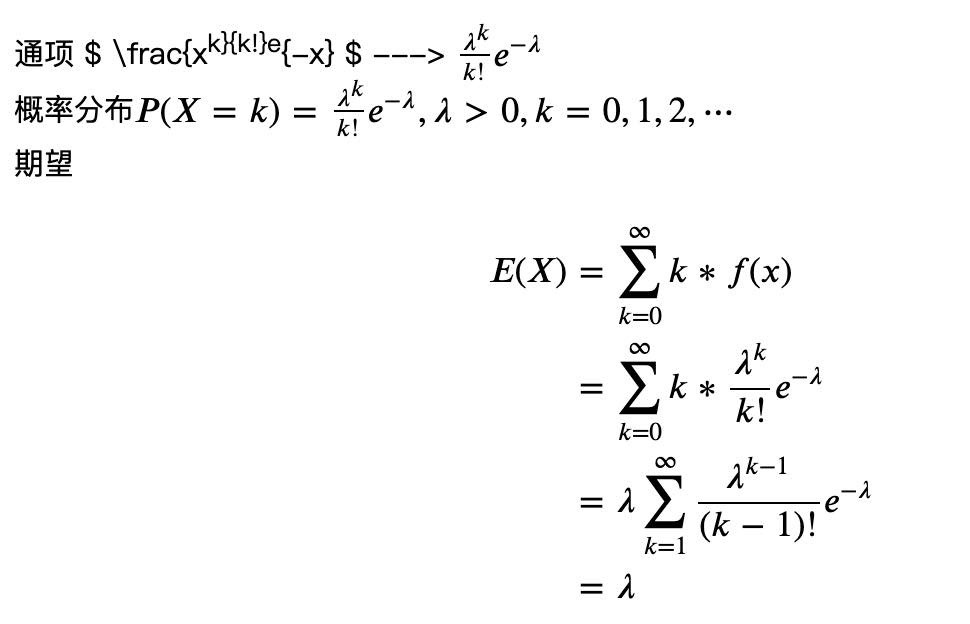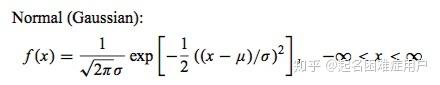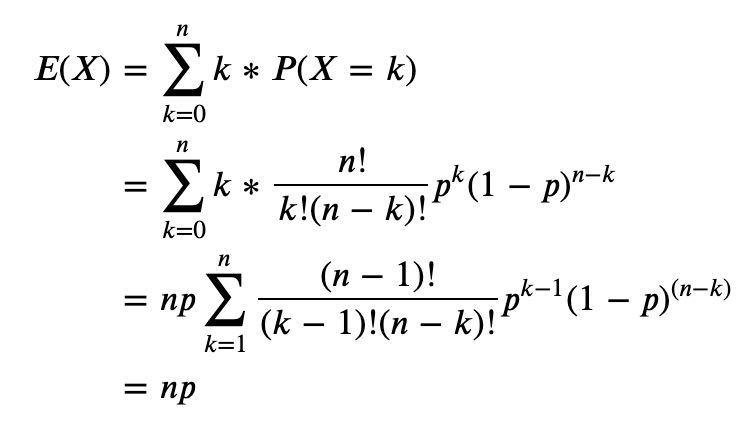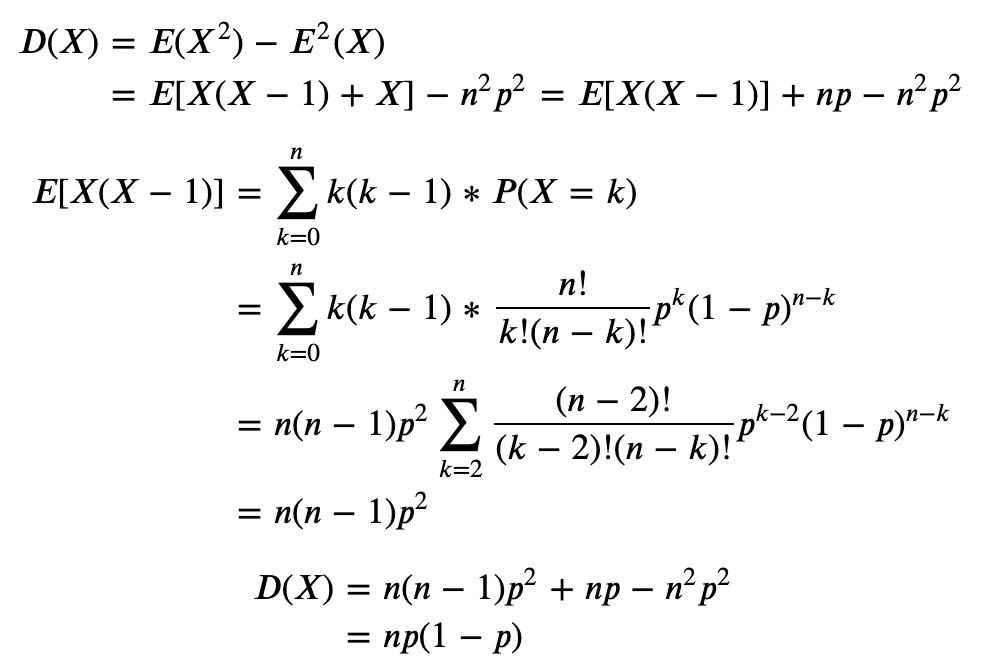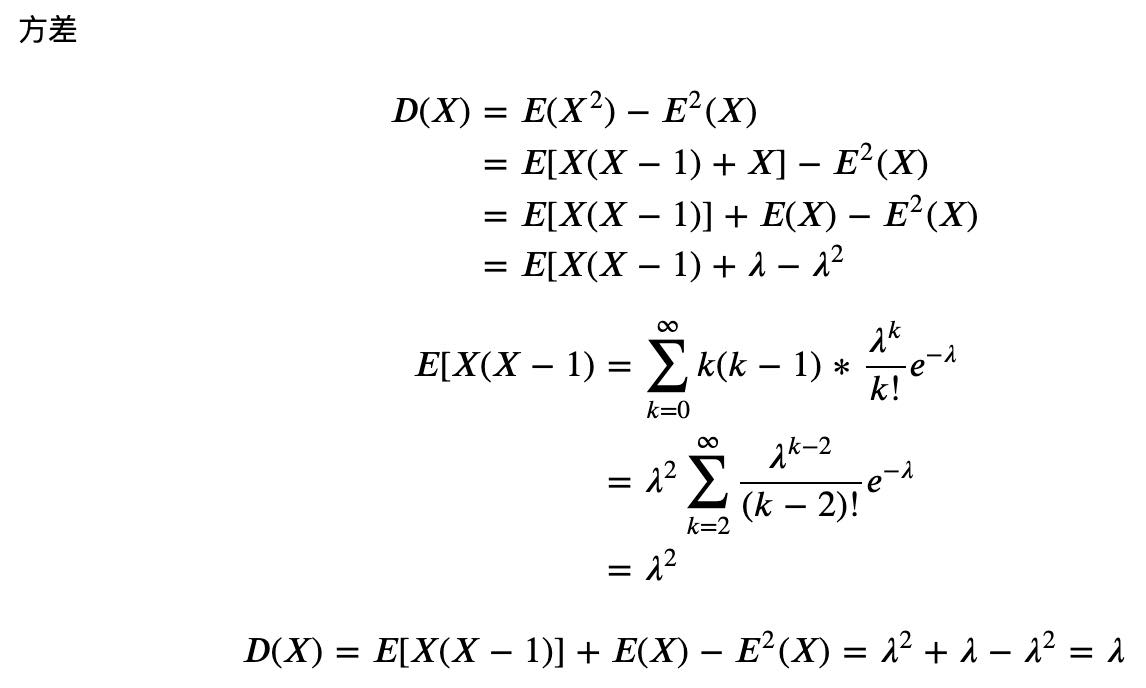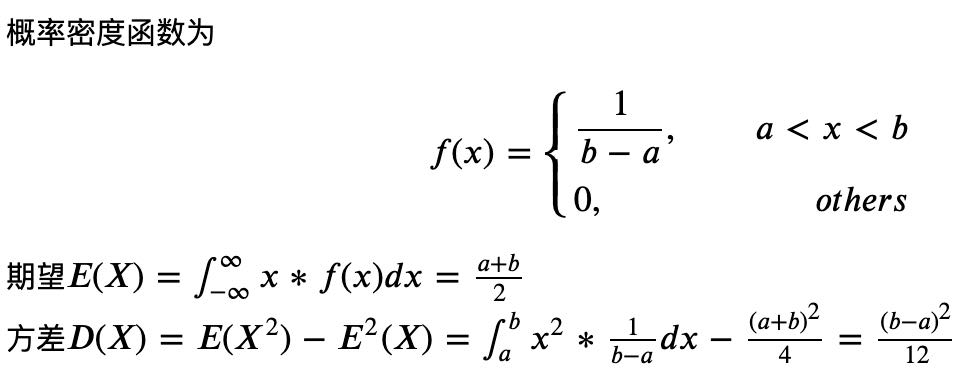常见概率统计分布及Python实现
一、离散随机变量及连续随机变量
随机变量
1. 离散随机变量(Discrete random variable):取值是可数个值(且只能为自然数0、1、2...)的随机变量
2. 连续随机变量(Continuous random variable):取值是一个区间中任一实数(即变量的取值可以是连续的)的随机变量
相应概率计算公式PMF/PDF/CDF
1. 离散随机变量:概率质量函数(Probability Mass Function,PMF)
PMF即离散随机变量在各特定取值上的概率
2. 连续随机变量:概率密度函数(Probability Density Function,PDF)
PDF:连续随机变量的概率密度函数是描述这个随机变量的输出值,在某个特定取值点附近可能性的函数。
3. 累积分布函数(Cumulative Distribution Function,CDF)
CDF:概率密度函数的积分,能完整描述一个随机变量X的概率分布。
概率中的PDF,PMF,CDF - wanzer之家 - CSDN博客
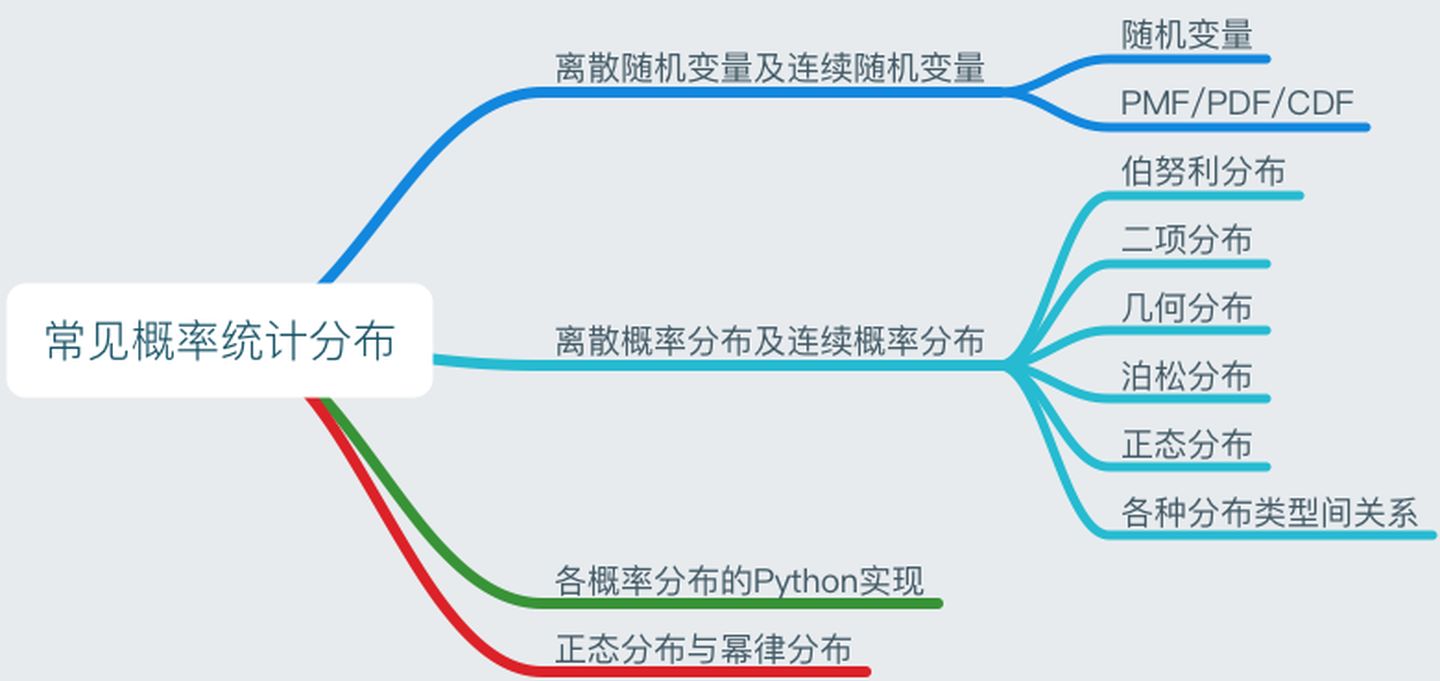
二、离散概率分布及连续概率分布
离散概率分布
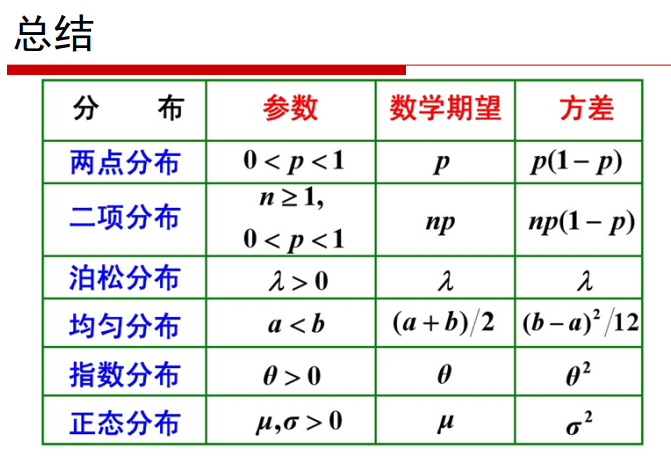
1. 伯努利分布(Bernoulli Distribution):亦称“0-1分布”
概念:一次试验,若成功随机变量取值为1,成功概率为p; 若失败随机变量取0,失败概率为1-p
期望𝐸(𝑋)=1∗𝑝+0∗(1−𝑝)=𝑝
方差 𝐷(𝑋)=𝑝∗(1−𝑝)2+(1−𝑝)∗(0−𝑝)2=𝑝(1−𝑝)
2. 二项分布(Binomial Distribution):即重复n次独立的伯努利实验,每次试验中只有两种可能的结果。
概念:进行n次伯努利试验。(n>=1),当n=1,二项分布就是伯努利分布
n次试验中总共成功的次数为k的概率 𝑃(𝑋=𝑘;𝑛,𝑝)=𝐶𝑘𝑛∗𝑝𝑘∗(1−𝑝)𝑛−𝑘
期望 𝐸(𝑋)=𝑛𝑝
期望的推导
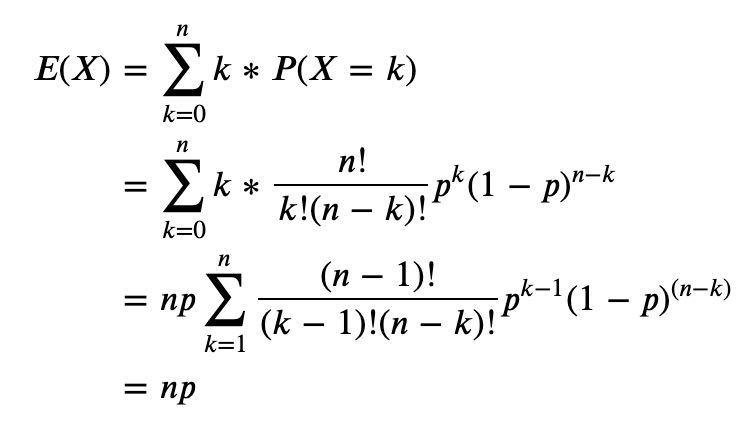
方差𝐷(𝑋)=𝑛𝑝(1−𝑝)
方差的推导
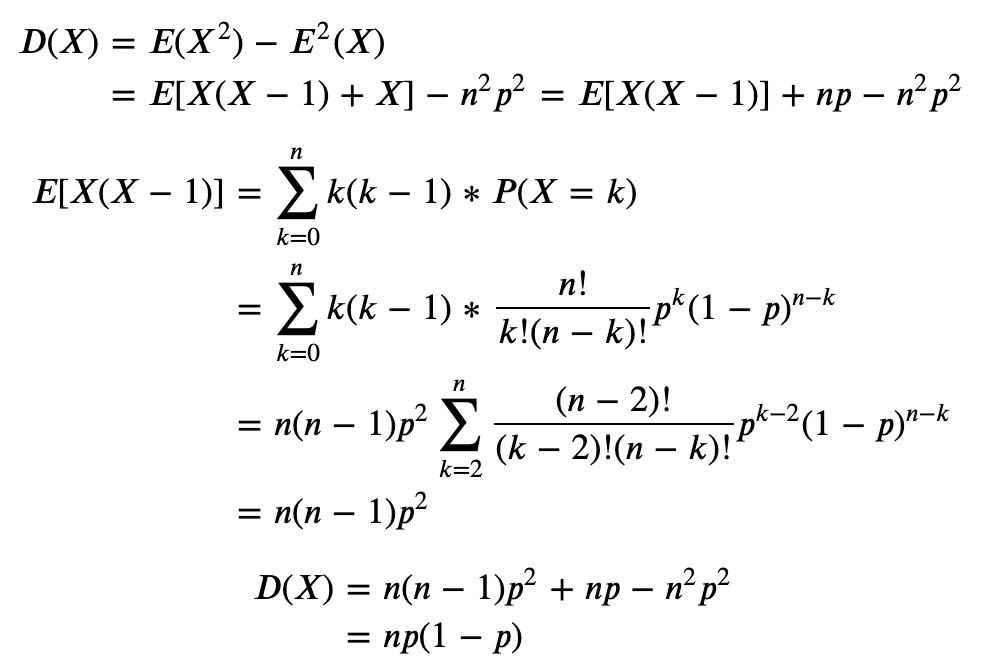
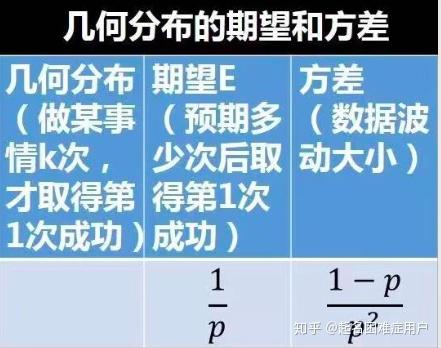
3. 几何分布(Geometric Distribution):在n次伯努利试验中,试验k次才得到一次成功的概率(即前k-1次均失败)
详细地说,是:前k-1次皆失败,第k次成功的概率。几何分布是帕斯卡分布当r=1时的特例。
几何分布的概率质量函数: 在伯努利试验中,成功的概率为p,若ξ表示出现首次成功时的试验次数,则ξ是离散型随机变量,它只取正整数,且有P(ξ=k)=p(1−p)k−1(k=1,2,…,0<p<1),此时称随机变量ξ服从几何分布。它的期望为1/p,方差为(1-p)/p2。
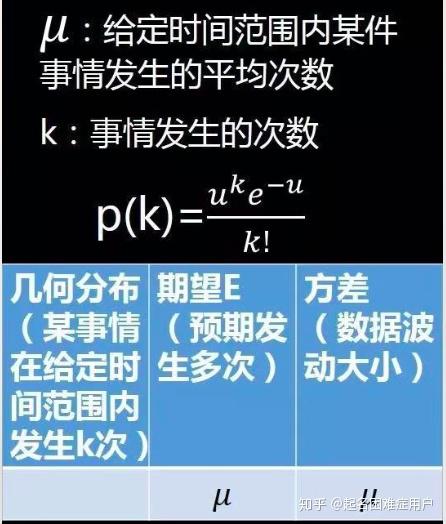
4. 泊松分布(Poisson Distribution):一种累计随机事件发生次数的最基本的独立增量过程。
泰勒展开式
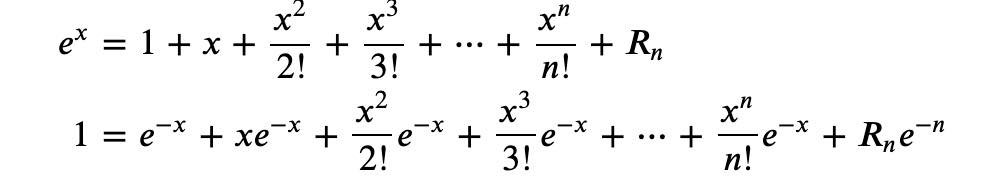
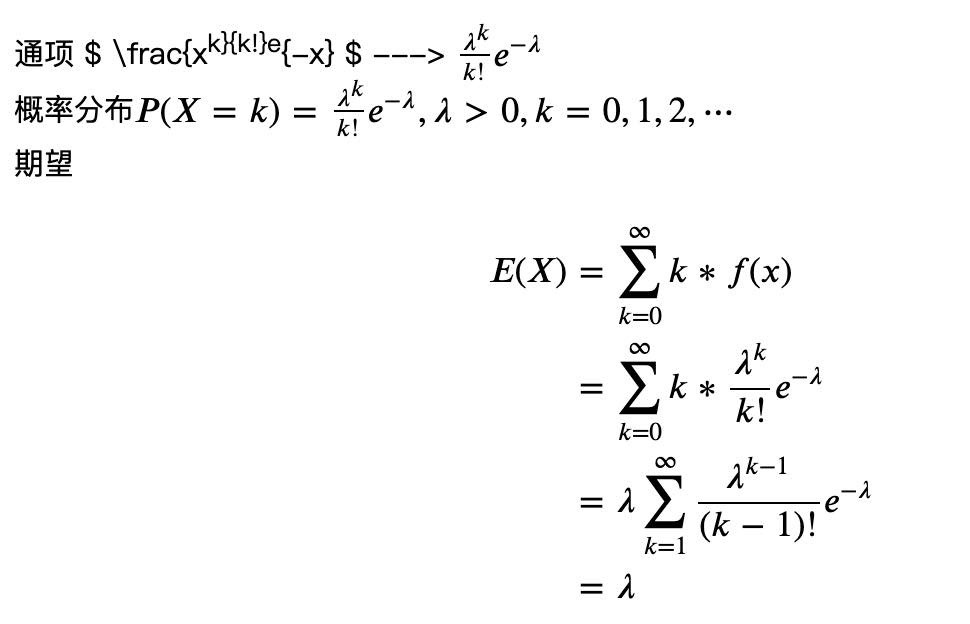
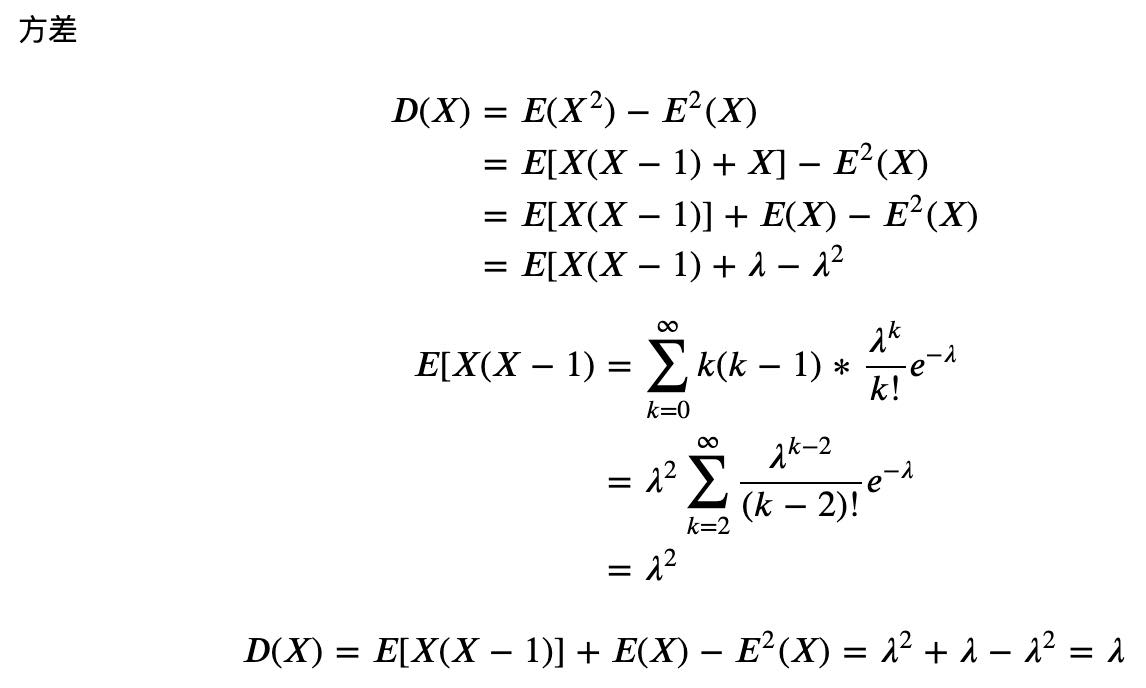
泊松分布一般需满足三个条件:事件的发生是小概率事件/事件间相互独立/事件发生的概率是稳定的, 泊松分布的期望和方差都是参数𝜆!
| import numpy as np
a = np.random.poisson(55,size=(4,))
print(a)
print(type(a))
>>> [46 50 39 57]
<class 'numpy.ndarray'>
|
连续概率分布
5. 均匀分布
如果连续型随机变量具有某种特定的概率密度函数,则称X服从[A,B]上的均匀分布(uniform distribution)
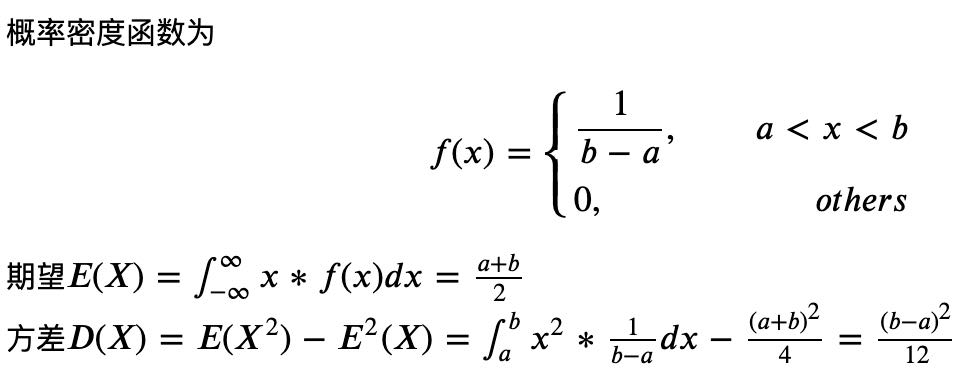
| #np.random.uniform(low=0.0, high=1.0, size=None)
a = np.random.uniform(20,50,size=(2,6))
print(a)
print(type(a))
>>> [[ 45.20217569 43.75312926 26.52703807 41.91200572 42.85374841
29.24479553]
[ 45.12516381 30.12544796 35.53555014 32.28527649 21.76682194
46.33104556]]
<class 'numpy.ndarray'>
|
指数分布(也称为负指数分布)是描述泊松过程中的事件之间的时间的概率分布,即事件以恒定平均速率连续且独立地发生的过程。 这是伽马分布的一个特殊情况。 它是几何分布的连续模拟,它具有无记忆的关键性质(Memoryless Property,又称遗失记忆性)。这表示如果一个随机变量呈指数分布,当s,t>0时有P(T>t+s|T>t)=P(T>s)。即,如果T是某一元件的寿命,已知元件使用了t小时,它总共使用至少s+t小时的条件概率,与从开始使用时算起它使用至少s小时的概率相等。

7. 正态分布/高斯分布(Normal Distribution):是所有分布趋于极限大样本的分布,属于连续分布。
正态曲线呈钟型,两头低,中间高,左右对称因其曲线呈钟形,因此人们又经常称之为钟形曲线。

| a = np.random.normal(40,3,size=(5,2))
print(a)
print(type(a))
>>>[[ 42.75053239 36.92362467]
[ 42.90588338 38.58249427]
[ 42.91278062 39.05507689]
[ 39.69794259 40.26237062]
[ 38.90643225 42.94278753]]
<class 'numpy.ndarray'>
|
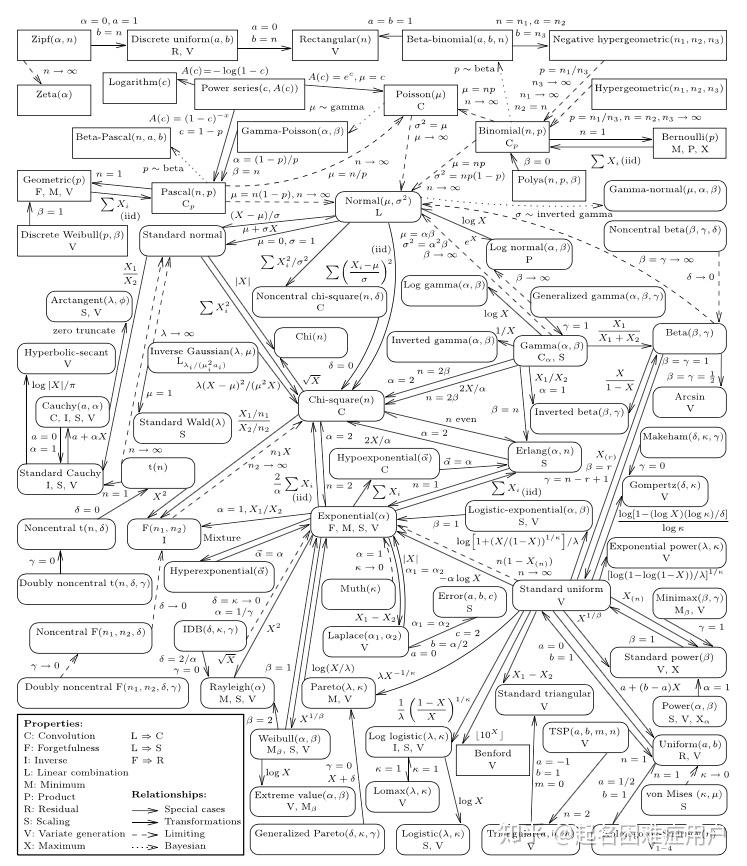
各种分布类型间关系
- 二项分布的极限分布是泊松分布。
- 泊松分布的极限分布是正态分布,即np=λ,当n很大时可近似相等。
- 二项分布和泊松分布都可以用正态分布代替(需满足一定条件,中心极限定理or大数定律)。
中心极限定理以及其和大数定律的区别 - CSDN博客
http://www.math.wm.edu/~leemis/2008amstat.pdf
以下为各单变量分布间关系:
各概率分布的Python实现:
| #导入包
import numpy as np #数组包
from scipy import stats #统计计算包的统计模块
import matplotlib.pyplot as plt #绘图包
%matplotlib inline
|
1.伯努利分布(Bernoulli Distribution)
| #1、定义随机变量:抛一次硬币,0代表失败即反面朝上;1代表成功即正面朝上
#(随机变量通常用大写字母表示)
X=np.arange(0,2,1)
X
>>>
array([0, 1])
#2、求对应分布的概率:概率质量函数(PMF:Probabilily mass function)
p=0.5 #硬币朝上的概率
pList=stats.bernoulli.pmf(X,p)
pList
>>>
array([0.5, 0.5])
#3、绘图
plt.plot(X,pList,linestyle='None',marker='o') #不需要将两点相连
plt.vlines(X,0,pList) #绘制竖线,参数说明plt.vlines(x坐标值,y坐标最小值,y坐标最大值)
plt.xlabel('随机变量:抛1次硬币结果为反面记为0,为正面记为1')
plt.ylabel('概率值')
plt.title('伯努利分布:p=%0.2f'%p)
|
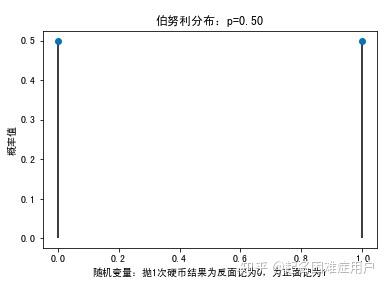
![]()
2.二项分布(Binomial Distribution)

| #1、定义随机变量:抛5次硬币,正面朝上的次数
n=5 #做某件事的次数
p=0.5 #做成功某件事的概率
X=np.arange(0,n+1,1)
X
>>>
array([0, 1, 2, 3, 4, 5])
#2、求对应分布的概率
pList=stats.binom.pmf(X,n,p) #参数含义为:pmf(k次成功,共n次实验,单次实验成功概率为p)
pList
>>>
array([0.03125, 0.15625, 0.3125 , 0.3125 , 0.15625, 0.03125])
#3、绘图
plt.plot(X,pList,linestyle='None',marker='o')
plt.vlines(X,0,pList)
plt.xlabel('随机变量:抛5次硬币,正面朝上的次数')
plt.ylabel('概率值')
plt.title('二项分布:n=%i,p=%0.2f'%(n,p))
|
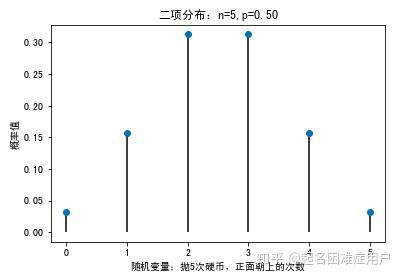
![]()
3.几何分布(Geometric Distribution)

| #1、定义随机变量:首次表白成功所需次数k
k=5 #做某件事的次数
p=0.6 #做成功某件事的概率
X=np.arange(1,k+1,1)
X
>>>
array([1, 2, 3, 4, 5])
#2、求对应分布的概率
pList=stats.geom.pmf(X,p) #参数含义为:pmf(第X次成功,单次实验成功概率为p)
pList
>>>
array([0.6 , 0.24 , 0.096 , 0.0384 , 0.01536])
#3、绘图
plt.plot(X,pList,linestyle='None',marker='o')
plt.vlines(X,0,pList)
plt.xlabel('随机变量:表白k次才首次成功')
plt.ylabel('概率值')
plt.title('几何分布:p=%0.2f'%p)
|
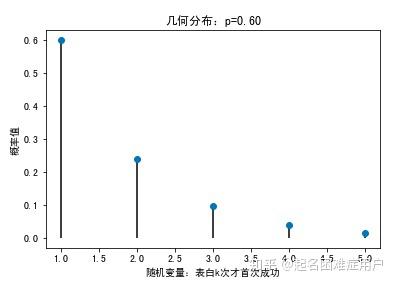
![]()
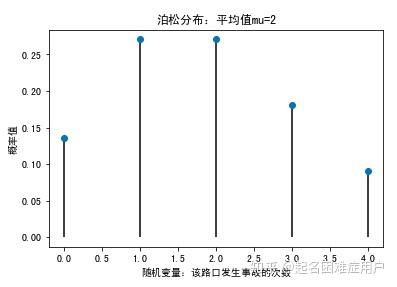
4.泊松分布(Poisson Distribution)
| #1、定义随机变量:已知某路口平均每天发生事故两次,则该路口一天内发生k起事故的概率是多少?
mu=2 #平均值:每天平均发生2起事故
k=4 #该路口发生4起事故的概率
X=np.arange(0,k+1,1)
X
>>>
array([0, 1, 2, 3, 4])
#2、求对应分布的概率
pList=stats.poisson.pmf(X,mu) #参数含义为:pmf(发生X次事件,平均发生mu次)
pList
>>>
array([0.13533528, 0.27067057, 0.27067057, 0.18044704, 0.09022352])
#3、绘图
plt.plot(X,pList,linestyle='None',marker='o')
plt.vlines(X,0,pList)
plt.xlabel('随机变量:该路口发生事故的次数')
plt.ylabel('概率值')
plt.title('泊松分布:平均值mu=%i'%mu)
|
![]()
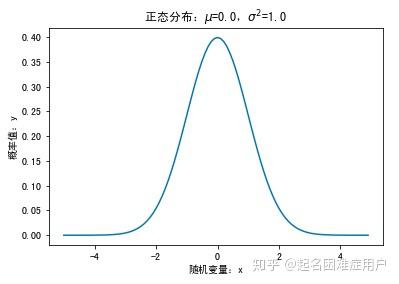
5.正态分布(Normal Distribution)
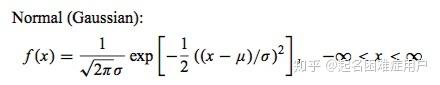
| #1、定义随机变量
mu=0 #平均值
sigma=1 #标准差
X=np.arange(-5,5,0.1)
#2、求对应分布的概率
pList=stats.norm.pdf(X,mu,sigma) #参数含义为:pdf(发生X次事件,均值为mu,方差为sigma)
#3、绘图
plt.plot(X,pList,linestyle='-')
plt.xlabel('随机变量:x')
plt.ylabel('概率值:y')
plt.title('正态分布:$\mu$=%0.1f,$\sigma^2$=%0.1f'%(mu,sigma))
|
![]()
5.4、已知正态分布查找对应概率值
分三步:确定分布范围、求标准分z值、查找z表格
1. 确定分布范围(以左尾为例)如:p(k<1.05)
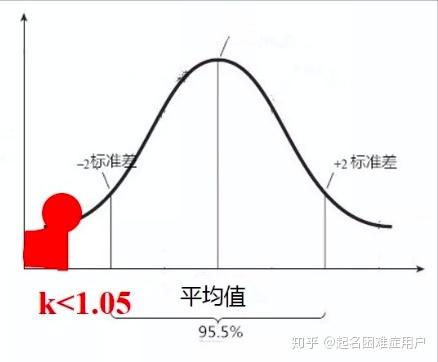
2. 求标准分 标准分z=(1.05-平均值)/标准差
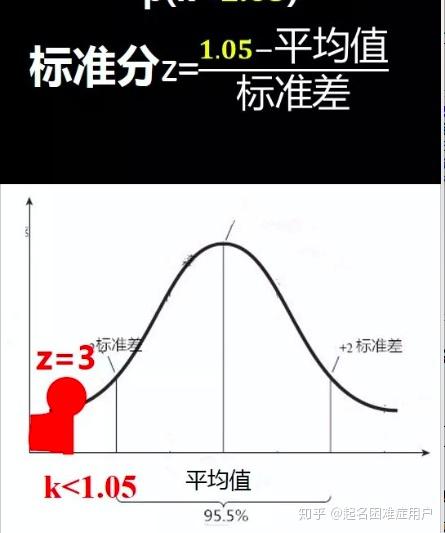
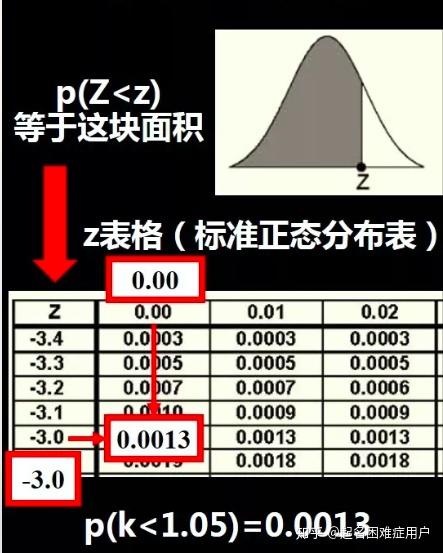
3. 查找z表格
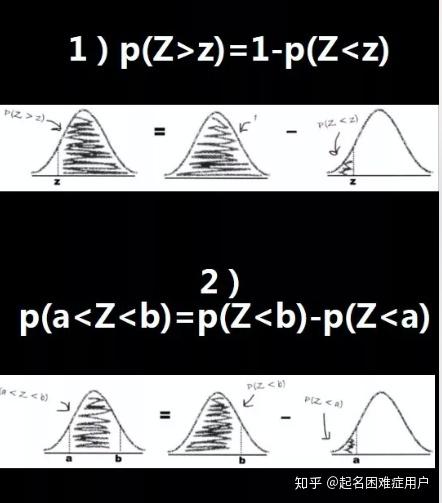
其他:右尾及双尾
三、正态分布与幂律分布
- 正态分布(Normal distribution)
正态曲线呈钟型,是两边低,中间高,左右对称曲线。一般而言,如果某个量是由许多微小的独立随机因素影响的结果,则可以认为该量符合正态分布。正态分布说明了事物运行有惯性的规律,能避免向另外的极端发展,从而体现出一种一定态势下的惯性波动。
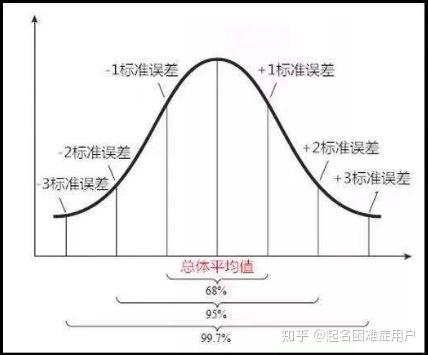
关于正态分布,你不知道它诞生之路是多么“变态”
- 幂律分布(Power law distribution)
幂律分布表现为斜率为负的幂指数的直线,概率越高,占比越小,生活中的马太效应及长尾分布都是幂律分布的典型案例。简单来说,幂律分布就是告诉你世界是不公平的,较少的人拥有大部分财富(二八法则),于是在他们身上就体现了财富的加速积累情况。
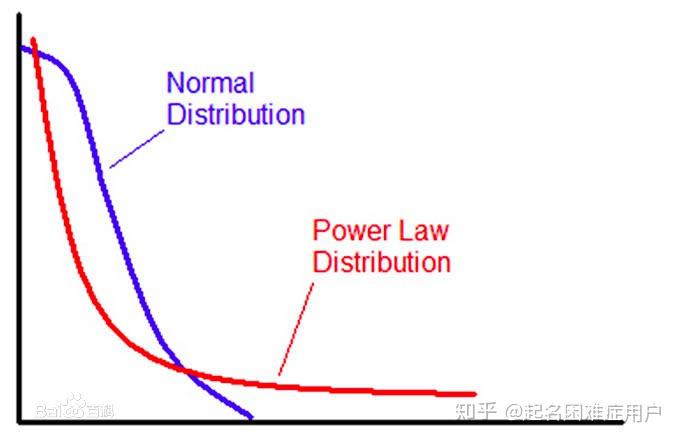
幂律分布 - Together_CZ的博客 - CSDN博客
凡本网注明"来源:XXX "的文/图/视频等稿件,本网转载出于传递更多信息之目的,并不意味着赞同其观点或证实其内容的真实性。如涉及作品内容、版权和其它问题,请与本网联系,我们将在第一时间删除内容!
作者: 起名困难症用户 https://zhuanlan.zhihu.com/p/53372254
作者: 米小粥 https://www.cnblogs.com/min2day/p/8013660.html