量化投资入门系列（八）——基于神经网络的股票走势预测¶

引言¶

近年来，神经网络在CV和NLP领域都实现了对传统的机器学习方法的降维打击，因此有人开始将神经网络应用到金融领域，以期取得超越传统机器学习方法的效果，而近年来各机构的实盘策略效果也没有让人失望，在合理的打标以及海量的因子构建的加持下，基于神经网络的策略取得了不俗的效果，本文将对神经网络在金融量化领域的应用进行阐述，前半部分会先进行一定的可行性分析，后面会具体阐述如何使用。

使用场景分析¶

赛道1：日间预测

在上一篇文章中，我们以xgboost为例介绍了机器学习在日间预测的应用，这其中有几方面对于最终的结果至关重要：打标、数据集划分以及因子质量。

xgboost对于异常值以及数据间数量级差异不敏感的特性使得其在因子的选择中如鱼得水，我们可以向模型中灌入大量的因子而不需要过多地关心其是否会影响模型的性能，另一方面，由于大部分技术类因子都由日间的数据构造成，因此基于这些因子的预测应用在日频、周频或月频调仓的策略上也比较合适。但是对于神经网络而言，在因子的使用中则无法如此地“随意”。从神经网络的原理上讲，其拟合过程需要依赖后向传播，这要求每一层网络都需要可导，因此一旦出现缺失值，网络随即崩溃，而对于缺失值的填充，方法众多，唯一的要义是要与被填充的因子本身的特性相匹配。而从神经网络最基本的单元上讲，无论CNN、RNN还是其他各种变体，本质上都是线性函数加激活函数的方式，而线性的模型，一个重要的特点就是希望输入的因子数据基本保持在相同的数量级上，因此神经网络在使用日间数据时的另一个重要步骤便是对因子的数量级进行处理，包括标准化、归一化以及取对数等。从上面的讨论中可以看出，如果只是单纯的利用截面因子去进行预测，神经网络相对于传统模型并没有体现出明显的优势，但是如果我们更改一下数据的使用方式，将神经网络的优势发挥出来，效果可能更加值得期待。对应传统的机器学习模型，其数据的输入都是1N的维度，N为因子数，而对于神经网络而言，其在这方面更加灵活，MN的输入维度赋予了神经网络更大的可能性，在预测的过程中，我们不再仅仅依赖当前截面的一些特征，而可以将历史的各个截面的信息一并地输入到模型中，使得未能被技术类因子所反映的历史数据能够被模型所应用，从而取得超越机器学习模型的效果。而更重要的是，由于有历史数据的数据，我们可能不再需要将大量利用历史数据所构造出的因子输入到模型中，而是依托于模型强大的拟合能力在前向传播的过程中就构造出有效的因子，这将帮我们从繁冗的因子数据处理中解放出来。

在日间的预测上，传统机器学习和神经网络可谓各有千秋，树模型对于因子有更高的宽容度，我们可以应用更多的因子，而神经网络则可以直接利用历史数据，打破人为因子构建的桎梏。而考虑到在中低频的策略中，我们除了关心标的在形态上的特征，更多地还会去关注标的的基本面信息，而这类数据通常都是季频更新的，因此在一定的时间区间内其并不会发生明显的变化，这将导致神经网络并不能很有效地去发挥自身的优势，甚至由于基本面数据在数量级及缺失上的问题，神经网络相对于树模型是具有一定的劣势的。

总体而言，在日间预测这一赛道上，神经网络可用性是没有问题的，只是优势不够明显，在计算资源并不丰富的情况下，低频策略并不一定非要上神经网络。

赛道2：日内预测

日内预测是完全不同于日间预测的一个领域，在日内预测中，我们可以更加专注于标的的技术形态的分析，而不需要过多地去关注基本面，在每一个tick，我们只需要关注当前的价量及盘口数据，然后结合当日的走势，进行短时的预测，说到这里，其实很清楚了，在日内预测这个领域，神经网络可谓是yyds，有着对其他模型的绝对优势，如果想尝试神经网络的预测，推荐从日内的预测入手。

在日内预测中，我们可使用的数据并不多，包括：

价格类：开盘价，最高价，最低价，最新价以及均价，对于价格序列的数据，可以制作成不同长度的K线，例如1minK线，5minK线等。
量能类：成交量、换手率。
盘口类：买盘加量分布，卖盘加量分布。
资金流向类：大单、小单以及超大单的分布等。

这些数据，有的可以直接用，有的需要进行一定的处理，以使得其能够保持在与其他数据相接近的数量级上，减少神经网络收敛的难度。

基于神经网络的模型构建¶

在框架选择上，tensorflow2.0集成了keras之后可用性明显提升，与pytorch上差别不大，本文后续的介绍都以pytorch为基础进行说明。

模型选择：RNN是否是最合适的结构

说到时间序列类的模型，几乎所有人的第一反应都是使用RNN类的网络，包括衍生的LSTM以及GRU等，但是如果仔细分析数据的特征，我们可能并不一定需要使用训练速度较慢的RNN类网络，解释如下：

RNN从诞生起便是为了处理普通神经网络无法处理定长的序列的问题，在RNN网络中，数据可以看做是一个截面一个截面的进入网络的，每一个截面的数据都与上一个截面输出的数据组合后进行输入，但是假如我们可以控制时间序列的长度，便并不需要特别的依赖这种一个截面一个截面输入的模式，而是将一整个时间序列的数据一口气的传给网络。

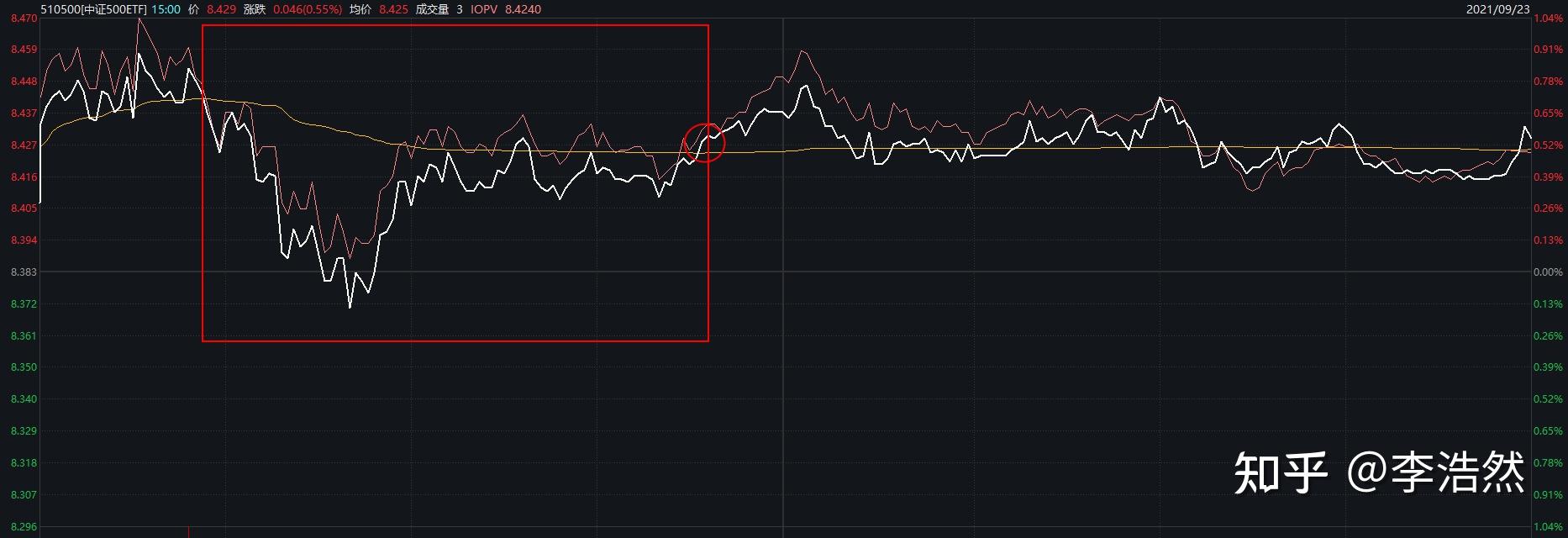
另一方面，我们可以考虑一下我们自己在分析走势时的行为，假如我们站在图中的圆圈位置进行预测，使用的数据是红框区间内的数据，在分析的过程中，我们自己的做法是直接看这一区间走势的整体情况，还是从左到右进行进行观察，很显然，我们并不需要一个个地观察，手工T0交易员在决策的过程中基本是观察最近一小段的走势，再结合最近一大段的走势来做出判断的。而同样的，在神经网络构建的过程中，从左到右的数据输入模式，可能也并不是那么地必要。

trend-stock-series-prediction-investing-_22Apr28160756400682_1.jpeg

既然RNN在此场景下的必要性并不强，那么我们是否可以使用效率更高的CNN呢，答案是肯定的，但是这并不意味着我们要把数据搞成图像的模式再输入到网络之中。从Tick数据的结构来看，假如我们选择使用M长度序列的数据，我们在任意时刻的可用数据都是MN的维度的，这其实与图像本身具备一定的相似度的，但是在使用上还是有一些差异。在图像领域，卷积核是二维移动的，但是在时间序列预测上，使用一维移动的卷积核可能更有效果，我们可以选择一个XN的卷积核，X为卷积的尺寸，然后让卷积核进行一维的移动，这样设计的原因是，在图像上，每个像素点，其实只是与其相邻的像素点来构成一定的特征的，但是在时间序列里，每个截面的数据之间并不具备空间关系，例如加入我们的数据格式是：开高收新均量换，我们显然不能说收盘价与跟成交量不存在关联。因此相对稳妥的做法是通过Cov1D来保证每一次卷积都将相关tick的所有数据被包含其中，从而重复应用各个数据之间的关系。

以上的讨论，旨在说明在模型的选择中，我们其实不必因为数据是时间序列而去使用RNN，完全可以将各种模型结构进行组合，尽管RNN是一个十分有效的处理时间序列的模型，但是CV在发展过程的各种创新其实也很值得去尝试，inception和ResNet中所采用的结构都可以应用到日内数据的预测中。而NLP中的一些结构同样值得借鉴，encoder-decoder的结构很显然比如简单的RNN来的更加有潜力，而相关的attention和Transformer等技术都是我们在模型构建过程中可以借鉴的结构。

多输入网络

如前文所述，对于tick数据，我们除了可以直接使用外，还可以构建成1minK线之类的数据，但是由此引发的问题是新构建的数据与原始数据的序列长度出现了差异，一种处理方式是构建的数据去使用更长的序列，从而保证长度的一致性，而另一种处理的方式就是构建多输入的网络，然后将多个通道的数据进行整合，再送入后续的网络中。

示例

如下是一个双输入网络的示例，包含了CNN和GRU两种结构，并且进行了一定的组合，这并不是一个直接可用的模型结构，但是解释了如何灵活地组合各种类型的模块。

import torch
from torch import nn

class ModelSample(nn.Module):
    def __init__(self, input_num, hidden_num, num_layers, bidirectional, output_num):

        super(ModelSample, self).__init__()
        self.hidden_size = hidden_num
        self.n_directions = 2 if bidirectional else 1  # 双向2、单向1
        self.num_layers = num_layers

        self.conv1 = nn.Conv1d(in_channels=input_num,
                               out_channels=hidden_num // 8,
                               kernel_size=5,
                               stride=1,
                               padding=0,
                               bias=True)
        nn.init.xavier_normal_(self.conv1.weight)
        nn.init.uniform_(self.conv1.bias)
        self.pool1 = nn.MaxPool1d(2, stride=2, padding=0)
        self.conv2 = nn.Conv1d(in_channels=hidden_num // 8,
                               out_channels=hidden_num // 4,
                               kernel_size=3,
                               stride=1,
                               padding=0,
                               bias=True)
        nn.init.xavier_normal_(self.conv2.weight)
        nn.init.uniform_(self.conv2.bias)
        self.pool2 = nn.MaxPool1d(2, stride=2)
        self.conv3 = nn.Conv1d(in_channels=hidden_num // 4,
                               out_channels=hidden_num // 2,
                               kernel_size=3,
                               stride=1,
                               padding=0,
                               bias=True)
        nn.init.xavier_normal_(self.conv3.weight)
        nn.init.uniform_(self.conv3.bias)

        self.GRU_layer = nn.GRU(input_size=hidden_num // 2,
                                hidden_size=36,
                                num_layers=num_layers,
                                bidirectional=bidirectional,
                                batch_first=True,
                                bias=True)

        for name, param in self.GRU_layer.named_parameters():
            if name.startswith("weight"):
                nn.init.orthogonal_(param)
            else:
                nn.init.uniform_(param)
        self.fc_g_1 = nn.Linear(36 * self.n_directions, hidden_num, bias=True)
        nn.init.xavier_uniform_(self.fc_g_1.weight)
        nn.init.uniform_(self.fc_g_1.bias)

        self.GRU_layer_2 = nn.GRU(input_size=50,
                                hidden_size=40,
                                num_layers=num_layers,
                                bidirectional=bidirectional,
                                batch_first=True,
                                bias=True)
        for name, param in self.GRU_layer_2.named_parameters():
            if name.startswith("weight"):
                nn.init.orthogonal_(param)
            else:
                nn.init.uniform_(param)
        self.fc_g_2 = nn.Linear(40 * self.n_directions, hidden_num, bias=True)
        nn.init.xavier_uniform_(self.fc_g_2.weight)
        nn.init.uniform_(self.fc_g_2.bias)

        self.fc_1 = nn.Linear(76, hidden_num, bias=True)
        nn.init.xavier_uniform_(self.fc_1.weight)
        nn.init.uniform_(self.fc_1.bias)
        self.fc_2 = nn.Linear(hidden_num, hidden_num // 2, bias=True)
        nn.init.xavier_uniform_(self.fc_2.weight)
        nn.init.uniform_(self.fc_2.bias)
        self.fc = nn.Linear(hidden_num // 2, output_num, bias=True)
        nn.init.xavier_uniform_(self.fc.weight)
        nn.init.uniform_(self.fc.bias)


    def forward(self, x1, x2):
        x_cnn = x1.view(-1, 1, self.hidden_size)
        conv1 = self.conv1(x_cnn)
        ac_conv = nn.Sigmoid()(conv1)
        pool1 = self.pool1(ac_conv)
        conv2 = self.conv2(pool1)
        ac_conv2 = nn.Sigmoid()(conv2)
        pool2 = self.pool2(ac_conv2)
        conv3 = self.conv3(pool2)
        ac_conv3 = nn.ReLU()(conv3)

        gru_output, hn = self.GRU_layer(ac_conv3)

        gru_output2, hn2 = self.GRU_layer2(x2)

        combine = torch.cat((hn, hn2), dim=1)

        fc_1 = self.fc_1(combine)
        dp_1 = nn.Dropout(p=0.3)(fc_1)
        activation_1 = nn.Sigmoid()(dp_1)
        fc_2 = self.fc_2(activation_1)
        dp_2 = nn.Dropout(p=0.3)(fc_2)
        activation_2 = nn.Sigmoid()(dp_2)
        fc_output = self.fc(activation_2)
        return fc_output

总结¶

使用神经网络进行股票走势的预测，最适用的场景是tick级的预测，而在模型的选择上，时间序列本身并不会把我们的选择限制在RNN类的模型上，我们可以充分的发挥个人的能动性，对应热门的网络结构都可以进行积极的尝试。

凡本网注明"来源：XXX "的文/图/视频等稿件，本网转载出于传递更多信息之目的，并不意味着赞同其观点或证实其内容的真实性。如涉及作品内容、版权和其它问题，请与本网联系，我们将在第一时间删除内容！
作者: 李浩然, 华泰证券算法工程师
来源： https://zhuanlan.zhihu.com/p/413092911